In Reinforcement Learning (RL) there is a big area of interest namely Markov Decision Processes (MDPS). In MDPS we are interested in processes that have Markov property.
In RL we have an agent which moves from states by taking actions at time to a different state . In simple terms the goal of the agent is to maximize its future rewards. That means it wants to take those actions that would lead to better rewards in expectation.
In order to design such processes we would need to identify the probability of being in states given all the previous states. If we do not have Markov Property this would look in mathematical terms as:
Now that we see that we would need to keep track of the complete state list where the agent has been to, which could make model design very complicated. This can be simplified when the processes have Markov Property.
The Markovian property says that the future state of a process depends only on the present state, not on how it got there (i.e., the past states). Which then implies:
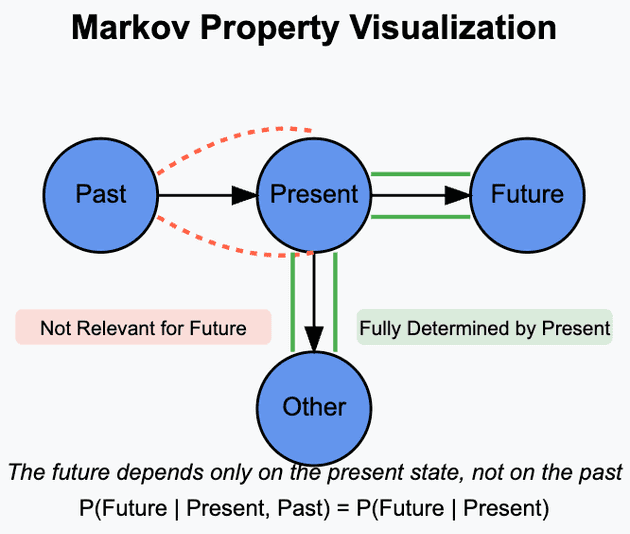
The image above shows that from Present state the system can transition to Future or Other states, which is entirely dependent on the Present state and independent of the past states.
This makes the process memoryless - only the current state matters for predicting the next one. How the agent reached the current state, which steps it took until now are not relevant for the next step.
Importance of Markov Property
- It makes the modeling of the process simple - we just need to keep track of the current state.
- Forms the basis for Markov Chains, that we have already looked into a little bit above.
- It leads to efficient computations.
Examples
- In a Board Game like Monopoly, your next position only depends on your current position and the dice roll. It doesn't matter how we got to that position. That makes it Markovian.
- Going from one train station to the next train station is only dependent on the current train station. How we got to the current train station is not relevant in planing where we can go to as the next station.
Finally, lets look at a Markovian Chain.
A Markov Chain is a mathematical model that describes a sequence of possible events where the probability of each event depends only on the current state and not on the sequence of events that preceded it.
Components of a Markov Chain
- States. All possible situations that the system can be in.
- Transition Probabilities. The chance of moving from one state to another.
- Initial State. Where the process starts.
Let us look at these components with an example:
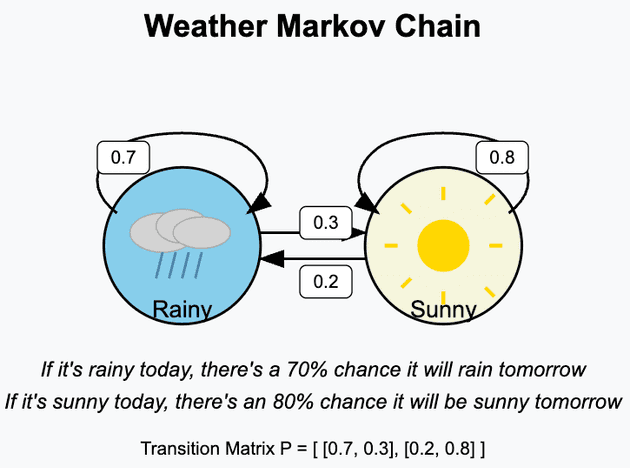
What we see in the image is a system of weather changes. We have two possible states that the system can be in Rainy or Sunny. What we additionally see is the transition matrix which can be written as following:
And the initial state could be rainy or sunny, it does not matter for this example.
In Summary, a Markov Chain is a way to model systems that move between states probabilistically. It obeys the Markov Property: the future only depends on the present, not the past. They're everywhere - from web algorithms to the weather to finance, example, Google PageRank, modeling credit rating etc.