Graphs

April 05, 2025

Have you ever used Google Maps, followed people on Instagram, or browsed Wikipedia? Then you've interacted with graphs - even if you didn't realize it!

Graphs help us model relationships and connections in the real world, from social networks to city maps to complex recommendation systems.

A graph is a collection of nodes (also called vertices) and edges (connections between nodes). Mathematically, graphs can be defined as:

A graph is a pair $G = (V, E)$ where $V = \text{vertices (or nodes)}$ and $E \subseteq V \times V = \text{edges}$ .

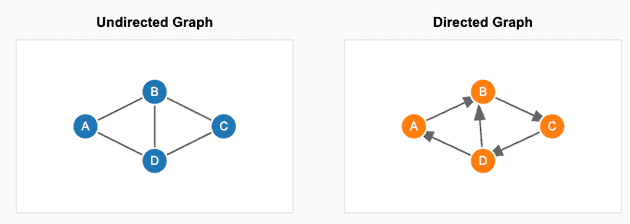
The edges of a graph can be undirected or directed, as seen below:

In the undirected graph above, it is possible not only to go from $A \rightarrow B$ but also to go from $B \rightarrow A$ . But in the directed graph above we can only go from $A \rightarrow B$ but there is no direct path from $B$ to $A$ .

Graphs can be represented as an adjacancy matrix $A$ . Where the entries $a_{ij}$ are 1s if and only if there is a edge from $V_i \rightarrow V_j$ . Example of an Adjacency matrix for the above two graphs can be seen below:

A_{undirected} = \begin{pmatrix} 0 & 1 & 0 & 1 \\ 1 & 0 & 1 & 1 \\ 0 & 1 & 0 & 1 \\ 1 & 1 & 1 & 0 \end{pmatrix}

Undirected graphs are symmetric.

A_{directed} = \begin{pmatrix} 0 & 1 & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \\ 1 & 1 & 0 & 0 \end{pmatrix}

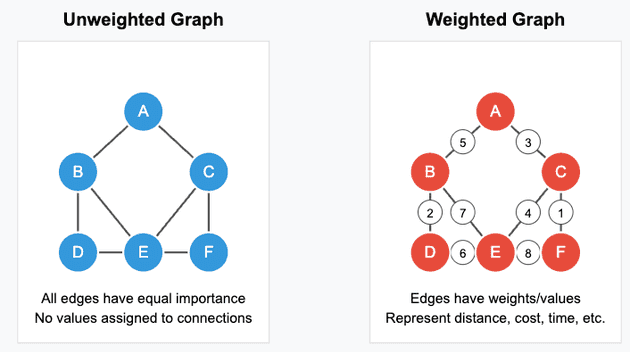
Another way of looking at graphs is if the edges have weights assigned to them. In that case not all the edges are treated equally. For example, let us consider the graph as road network. Not each road is of the same length, so if we want to calculate the time that we need to go from one point to another, we need to take into account the lengths of individual edges (roads) that we may come accross during our journey.

Why are graphs important? Graphs are everyhwere. They help solve many problems like:

shortest or quickest path between two points,
connectivity - can everyone be reached in a network
recommendation systems - what should you buy next, whom should you follow next.

They are used in search engines, logistics and transporation, biology, chemistry and artificial intelligence.

Graphs are really interesting, and can be used to represent many different things. For example we represented weather markov chain in my previous blog post as weighted graphs, where the transition probilities between states was the weight assigned to the edges. Hidden markvo models can also be represented in the form of graphs.

We will have a look at graph algorithms in some other post in the future.